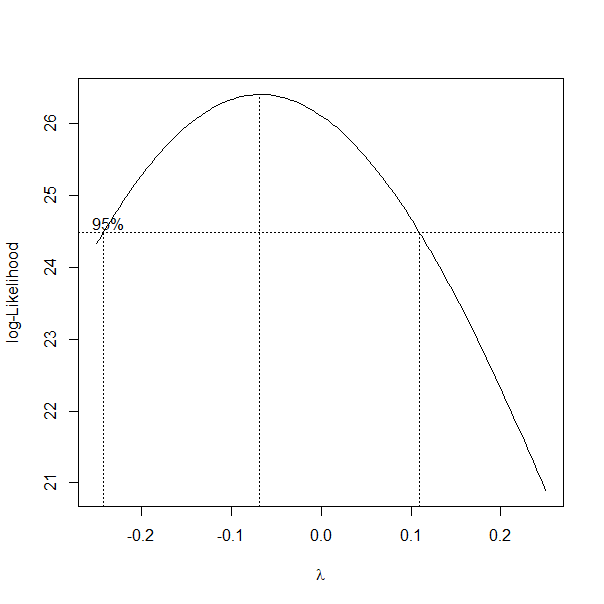Usually transformation to numeric data $\mathcal{D}={X_i,Y_i}_{i=1}^n$ is necessary in regression analysis, usually to stablize variance. Box-Cox is the most important method. \(\begin{align} Y^*=\dfrac{Y^\lambda -1}{\lambda }\mathrm{e.g.}=\begin{cases} Y^*\sim Y &,\lambda =1\\ Y^*\sim \sqrt{Y} &,\lambda =0.5\\ Y^*\sim \ln Y &,\lambda =0\\ Y^*\sim 1\big/ Y &,\lambda =-1 \end{cases} \end{align}\)
with linear model \(\begin{align} Y^*=X'\beta^* +\varepsilon^* ,\quad \varepsilon^* \sim N(0,\sigma ^2) \end{align}\)
where $X=(1,X_1,\ldots,X_p)’$, $\beta ^*=(\beta _0,\beta _1,\ldots,\beta _p)’$
Likelihood function expressed in $\mathcal{D}={X_i,Y_i^*}_{i=1}^n$: \(\begin{align} L(\beta^* ,\sigma ^2;\lambda )=\dfrac{1}{(2\pi\sigma ^2)^{n/2}}\exp\left[ -\dfrac{1}{2\sigma ^2}\sum_{i=1}^n\left( Y_i^*-X_i'\beta^* \right)^2 \right] \left|J\left(\dfrac{\partial^{} Y^*}{\partial Y^{}}\right)\right| \end{align}\)
where the Jacobi matrix could be denoted in Geometric Mean $\mathrm{GM}(Y )=\prod_{i=1}^n Y_i^{1/n} $ \(\begin{align} \left|J\left(\dfrac{\partial^{} Y^*}{\partial Y^{}}\right)\right|=\prod_{i=1}^nY_i^{\lambda -1}\mathrm{GM}\left( Y \right) ^{n(\lambda -1)} \end{align}\)
MLE estimators are similar: \(\begin{align} \hat{\beta }^*=&(X'X)^{-1}X'Y^*\\ \hat{\sigma }^2_n=&\dfrac{1}{n}\sum_{i=1}^n(Y_i^*-\bar{Y}^*) \end{align}\)
Subtitute MLE estimators back to (log-)likelihood: \(\begin{align} \log L(\beta ,\sigma ^2;\lambda )=\ell(\lambda )=-\dfrac{n}{2}\log \dfrac{\hat{\sigma }^2_n}{\mathrm{GM}(Y)^{2(\lambda -1)} }+\mathrm{const} \end{align}\)
By plotting $\ell(\lambda )$ v.s. $\lambda $ we could locate a $\lambda $ both appropriate in interpretability and likelihood maximization. Here’s the example code from r::MASS, which indicating a selection of $\lambda =0$ for logarithm transformation.
library(MASS)
boxcox(Volume ~ log(Height) + log(Girth), data = trees,
lambda = seq(-0.25, 0.25, length = 10))